Faster Enumeration-based Lattice Reduction

Our paper “Faster Enumeration-based Lattice Reduction: Root Hermite Factor in Time ” – together with Shi Bai, Pierre-Alain Fouque, Paul Kirchner, Damien Stehlé and Weiqiang Wen – is now available on ePrint (the work has been accepted to CRYPTO 2020). Here’s the abstract:

We give a lattice reduction algorithm that achieves root Hermite factor in time and polynomial memory. This improves on the previously best known enumeration-based algorithms which achieve the same quality, but in time . A cost of was previously mentioned as potentially achievable (Hanrot-Stehlé’10) or as a heuristic lower bound (Nguyen’10) for enumeration algorithms. We prove the complexity and quality of our algorithm under a heuristic assumption and provide empirical evidence from simulation and implementation experiments attesting to its performance for practical and cryptographic parameter sizes. Our work also suggests potential avenues for achieving costs below for the same root Hermite factor, based on the geometry of SDBKZ-reduced bases.

Concretely, this work reduces the cost of enumeration-based, i.e. polynomial memory, BKZ-k in dimension from to

In the plot below “Alg. 3” is our new algorithm (well, our “practical variant”), “Fig. 2” refers to the cost and “Alg. 3, free preprocessing” is a plausible lower bound for our new “practical-variant” algorithm.

Speaking of lower bounds, if we assume free preprocessing then we can go even below the leading constant of which was previously established as heuristic lower bound for enumeration-based algorithms:

The key idea behind our algorithm is that enumerating over a typical HKZ shape (red-ish part in the plot below) has cost but enumerating over a shape corresponding to the Geometric Series Assumption (GSA, green-ish part in the plot below) has cost .

Thus, we need to make sure enumeration sees something more like the green-ish shape rather than the red-ish shape. To make that happen in (SD)BKZ, we preprocess a larger block than we enumerate over to push the “not so nice” part out of the enumeration window (FWIW I pitched the name “procrastinating BKZ” for that to my coauthors but they weren’t convinced):

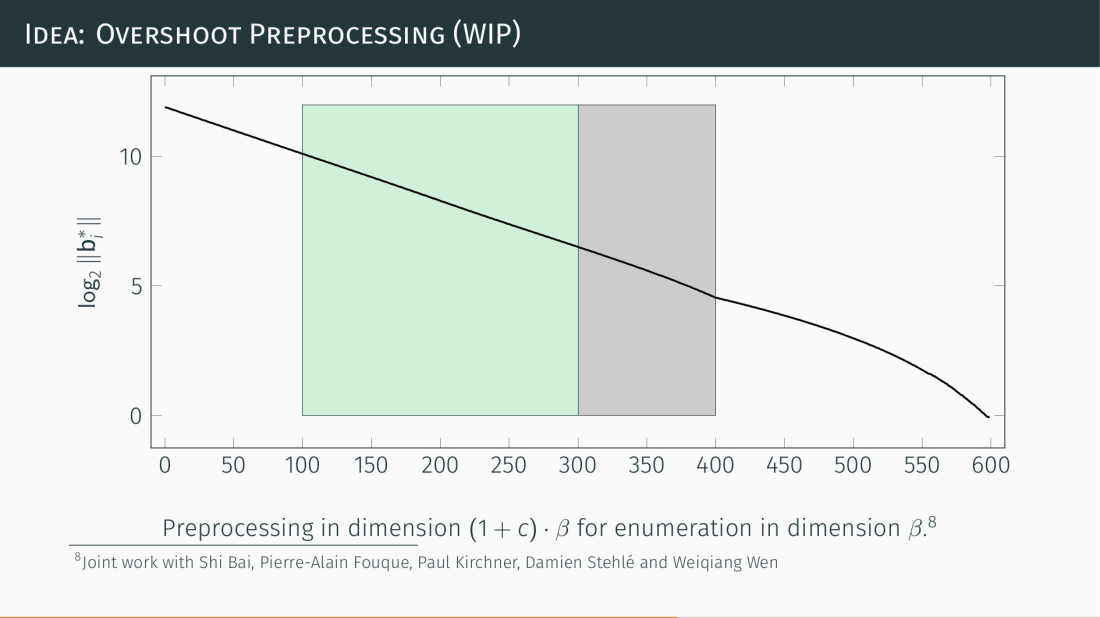
Btw. the two slides above are from my talk at the Simon’s Institute where I explained (amongst other things) the key idea behind our algorithm.

Now, to explain how we can beat (assuming free preprocessing!) note that the beginning of the red-ish typical HKZ shape is flatter (i.e. “nicer”) than the green-ish GSA part. Thus, the optimal choice is to enumerate over a mix of those two. However, while we know how to recursively produce a GSA shape to achieve , we do not know how to do the same to produce the shape for a complexity of .

PS: The ePrint paper not only contains all the raw data in our plots as an attachment but also the FPyLLL-based source code of our simulations and implementations.