meataxe64

Meataxe64 is a large software development project to produce programs for working at high performance with large matrices over finite fields.

At the lowest level, the aim is to work modulo primes (only), using grease (much like “four Russians”) to reduce the amount of work, to use vectorized code in x86 assembler (SSE/AVX) to do the basic operations and to have short rows and few columns so that matrices fit suitably into the various levels of cache. The objective is to run as fast as possible with as little use of real-memory bandwidth as possible.

At a middle level, the aim is to use linear functions to work with extension fields, and to chop the matrices up so that the lowest level can operate.

At a higher level, the aim is to make effective use of a multi-core environment, building on the advantage that the cache-friendly lower level provides to ensure that many cores can be used effectively. The thread-farm looks after the messy signals, locks and thread handling.

It is hoped soon that a layer will be added to take a matrix that fits on disk but not in memory to extend the possible scale of operations further.

Finally I dream that a fault-tolerant distributed system can be build on top of this to handle matrices of gargantuan proportions, but this lies some considerable way into the future.

Go read the development blog, I certainly learned a lot from Richard Parker whenever we talked.

Enrico Bertolazzi’s linear algebra code over GF(2) available

Enrico made the code (if the link doesn’t work search for his name on Research Gate) for his LU factorisation code over GF(2) available online under the GPL. This is an implement of the algorithm described by Anna and him in Fast matrix decomposition in F2 and for which they give timings in that paper (discussed a bit here). I had to fix some includes to make it compile on my box, but nothing major. I can also confirm the impressive performance of their software (I ran testRankComputation).

Continue reading “Enrico Bertolazzi’s linear algebra code over GF(2) available” →

Sage 5.10

Sage 5.10 was released earlier today. It has the following goodies I particularly care about:

Faster Dense Linear Algebra over GF(2)

TL;DR: We updated M4RI to the most recent upstream release which is better suited for modern CPUs.

After Enrico Bertolazzi and Anna Rimoldi kicked out butts with their pre-print we went to work to re-tune M4RI. That is, I don’t agree with their premise that their new algorithm is the (main) cause of their impressive performance. As a result M4RI got considerably faster on modern CPUs.

Here’s a comparison of Sage 5.8 (which has the same performance characteristics as 5.9 for this stuff) and Sage 5.10. Sage 5.8 goes first:

sage: A = random_matrix(GF(2),2^14, 2^14)
sage: B = random_matrix(GF(2),2^14, 2^14)
sage: %time A*B
CPU times: user 4.46 s, sys: 0.02 s, total: 4.48 s
Wall time: 4.50 s

sage: %time A.echelonize()
CPU times: user 2.53 s, sys: 0.00 s, total: 2.53 s
Wall time: 2.54 s

Now Sage 5.10 which is 1.22 times faster for multiplication and 1.17 times faster for elimination in this particular benchmark.

sage: A = random_matrix(GF(2),2^14, 2^14)
sage: B = random_matrix(GF(2),2^14, 2^14)
sage: %time A*B
CPU times: user 3.61 s, sys: 0.04 s, total: 3.65 s
Wall time: 3.66 s

sage: %time A.echelonize()
CPU times: user 2.16 s, sys: 0.00 s, total: 2.17 s
Wall time: 2.17 s

For comparision, Magma 2.15-10 takes 4.5 seconds for this multiplication and Magma 2.18-7 takes 5 seconds on the same machine. See here for details on the M4RI update.

Faster Dense Linear Algebra over GF(2^e)

TL;DR: Improvements over GF(2) have a knock-on effect on GF(2^e) and we upgraded M4RIE to the newest upstream release which extends the supported degree size up to $e \leq 16$

M4RIE recently dropped its dependency on Givaro and extended the degrees it supports up to 16. Sage 5.10 updates to this new release and extends the finite field size that is covered by M4RIE to 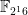$\mathbb{F}_{2^16}$ . This means a huge performance improvements for dense linear algebra over 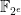$\mathbb{F}_{2^e}$ for $8 < e \leq 16$ . Note, however, that these cases are not fully optimised yet, so that it’s not the fastest implementation – in this range – yet. Sage 5.8 first:

sage: A = random_matrix(GF(2^8,'a'),10^4, 10^4)
sage: B = random_matrix(GF(2^8,'a'),10^4, 10^4)
sage: %time A*B
CPU times: user 32.07 s, sys: 0.48 s, total: 32.56 s
Wall time: 32.67 s
10000 x 10000 dense matrix over Finite Field in a of size 2^8

sage: A = random_matrix(GF(2^12,'a'),10^3, 10^3)
sage: B = random_matrix(GF(2^12,'a'),10^3, 10^3)
sage: %time A*B # Sage 5.8 uses generic Python code to do this
CPU times: user 339.02 s, sys: 0.70 s, total: 339.72 s
Wall time: 340.86 s
1000 x 1000 dense matrix over Finite Field in a of size 2^12

Now, Sage 5.10 which is 1.16 times and 1420 times faster respectively for these benchmarks.

sage: A = random_matrix(GF(2^8,'a'),10^4, 10^4)
sage: B = random_matrix(GF(2^8,'a'),10^4, 10^4)
sage: %time A*B # knock-on effect from GF(2) improvements
CPU times: user 27.42 s, sys: 0.62 s, total: 28.04 s
Wall time: 28.14 s
10000 x 10000 dense matrix over Finite Field in a of size 2^8

sage: A = random_matrix(GF(2^12,'a'),10^3, 10^3)
sage: B = random_matrix(GF(2^12,'a'),10^3, 10^3)
sage: %time A*B # new code in M4RIE
CPU times: user 0.23 s, sys: 0.01 s, total: 0.24 s
Wall time: 0.24 s
1000 x 1000 dense matrix over Finite Field in a of size 2^12

For comparison, Magma 2.15-10 takes 3.79 seconds and Magam 2.18-7 takes 0.16 seconds for the latter benchmark. This highlights that M4RIE isn’t what it should be yet in that range (see here for details).

A Learning With Errors Instance Generator

I’ve written about it here.

Matrix Multiplication over GF(p^e)

After my talk at Sage Days 35 in Warwick (that was in winter 2011) David Harvey had an idea on how to speed up matrix multiplication over $\mathbb{F}_{p^n}$ . We spend some time on this in Warwick and developed this idea further (adding fun stuff like Mixed Integer Programming in the process) but did not get around to do much on this project in the mean time (I have explained the idea at the end of my talk in Mykonos, though).

Just now, in a conversation with Richard Parker I was reminded of this dormant project, i.e., the question of how many multiplications i $\mathbb{F}_p$ it takes to do a multiplication in $\mathbb{F}_{p^n}$ . In particular, I recalled to have written some code for Sage which gives some upper bound to this answer which is better than Karatsuba.

Well, here’s an interactive demo … gosh, I love the Sage cell server.

M4RI 20121224

I have just pushed the button to release M4RI 20121224. The main feature of this release is a considerable performance improvement. It all started with Fast matrix decomposition in F2 by Enrico Bertolazzi and Anna Rimoldi showing up on the arXiv. Here’s the abstract

In this work an efficient algorithm to perform a block decomposition (and so to compute the rank) of large dense rectangular matrices with entries in F2 is presented. Depending on the way the matrix is stored, the operations acting on rows or block of consecutive columns (stored as one integer) should be preferred. In this paper, an algorithm that completely avoids the column permutations is given. In particular, a block decomposition is presented and its running times are compared with the ones adopted into SAGE.

… and that comparison made M4RI (which realises this functionality in Sage) look pretty bad. I did’t (and still don’t) share the implicit assumption that avoiding column swaps was the key ingredient in making this code so much faster than ours. I assume the impressive timings are due to a very efficient base case implementation. Anyway, we sat down and looked for performance bottlenecks the result of which is 20121224. I actually have no idea whether we caught up to the code described in Enrico’s and Anna’s pre-print as they did not publish their sources.

Still, the performance improvements over 20120613 were worth the trouble. Below two plots of the (normalised) leading constants giving the leading constants for multiplication and elimination respectively (more plots on imgur) That is, it plots the running time divided by $n^{2.807} \cdot 10^9$ . In theory these plots should all have slope 0.

Finally, here’s the plot for Fast matrix decomposition in F2 which starts very small but has a rather large slope. That’s why I concluded that the performance stems from a very efficient base case. I should get in touch with Enrio and Anna about this.

M4RIE: support for finite fields up to degree 16 added

I committed support for finite fields up to degree 16 to M4RIE a few days ago. Furthermore, the dependency on Givaro for constructing finite fields was dropped.

Don’t get me wrong. Givaro is a fine library, much better than what I wrote for M4RIE. However, it is a C++ library while M4RIE is a C library and the little functionality of finite field arithmetic needed in M4RIE was not that hard to add natively. In the past M4RIE relied on Givaro for running tests and benchmarks, the core library was always free of C++. However, as we plan to add support for high-degree polynomials over matrices over $\mathbb{F}_2$ , we need the ability to create finite extensions of $\mathbb{F}_2$ on the fly in the core library.

Continue reading “M4RIE: support for finite fields up to degree 16 added” →

Linear Algebra for Gröbner Bases over GF(2): M4RI

Two days ago I wrote about LELA’s implementation of Gaussian elimination for Gröbner basis computations over $\mathbb{F}_2$ . Yesterday, I implemented LELA’s algorithm (which is from Faugere & Lachartre paper) in M4RI. Continue reading “Linear Algebra for Gröbner Bases over GF(2): M4RI” →

Linear Algebra for Gröbner Bases over GF(2): LELA

The Efficient Linear Algebra for Gröbner Basis Computations workshop in Kaiserslautern two weeks ago was a welcome opportunity to finally test out LELA, a library specifically written for linear algebra for Gröbner basis computations including for GF(2). The library implements the “Faugère-Lachartre” algorithm (a similar trick, though less developed, appeared before in PolyBoRi) and uses M4RI for dense parts over GF(2).

So, I ran my benchmark matrices through LELA, discovered a bug in the process, then Bradford returned the favour and discovered a bug in M4RI … Finally, below are the timings. The column PLE is the PLE algorithm as implemented in M4RI, M4RI is the M4RI algorithm as implemented in M4RI, GB is a very naive variant of the algorithm LELA uses and LELA is, well, LELA.

problem	m	n	density	PLE	M4RI	GB	LELA
HFE 25	12307	13508	0.076	1.0	0.5	0.8	0.56
HFE 30	19907	29323	0.067	4.7	2.7	4.7	3.42
HFE 35	29969	55800	0.059	19.3	9.2	19.5	13.92
Mutant	26075	26407	0.184	5.7	3.9	2.1	12.07
n=24, m=26	37587	38483	0.038	20.6	21.0	19.3	7.72
n=24, m=26	37576	32288	0.040	18.6	28.4	17.0	4.09
SR(2,2,2,4) c	5640	14297	0.003	0.4	0.2	0.1	0.40
SR(2,2,2,4) c	13665	17394	0.013	2.1	3.0	2.0	1.78
SR(2,2,2,4) c	11606	16282	0.035	1.9	4.4	1.5	0.81
SR(2,2,2,4)	13067	17511	0.008	1.9	2.0	1.3	1.45
SR(2,2,2,4)	12058	16662	0.015	1.5	1.9	1.6	1.01
SR(2,2,2,4)	115834	118589	0.003	528.2	578.5	522.9	48.39

What this table means is that one can expect more than an order of magnitude of speed-up when using LELA – which is dedicated to these computations – instead of M4RI – which does not have the specialised algorithm implemented yet. For very small matrices sometimes M4RI/PLE win, but then not by a large margin. The only row where LELA doesn’t do so good is Mutant, which – btw. – is not an F4 matrix but comes from the MXL2 algorithm. It is possible that LELA’s sparse data structures are not that well equipped to deal with this rather dense matrix.

I am in the process of implementing the algorithm LELA uses in M4RI and will report updated timings here.

Report: Workshop on Efficient Linear Algebra for Gröbner Basis Computations

As you may know, today is the last day of the wokshop on Efficient Linear Algebra for Gröbner Basis Computations that Christian Eder, Burcin Eröcal, Alexander Dreyer and I organised.

I have to say that I am quite pleased with how the workshop played out. We planned the whole thing to be hands on: people were strongly encouraged to work on projects, i.e., to write code preferably together, in addition to attending talks. Those who attended a Sage Days workshop in the past, will know what workshop format I am referring to. Continue reading “Report: Workshop on Efficient Linear Algebra for Gröbner Basis Computations” →

Efficient Linear Algebra for Gröbner Basis Computations – June 4-8, 2012 – Kaiserslautern, Germany

Linear algebra plays an important role in modern efficient implementations of Gröbner basis algorithms. Consequently, a number of groups aim at developing linear algebra packages for these computations: we mention the HPAC project, LELA by the Singular team, the FGB package by Jean-Charles Faugère, the M4RI libraries, specialised linear algebra routines in PolyBoRi as well as non-public projects. In this workshop we want to bring researchers interested in this problem and developers of these packages together to discuss and develop solutions. The format of this workshop will be a mixture of talks, coding sprints and design discussions.

Topics will include but are not limited to:

presentation of existing software packages and solutions for linear algebra suitable for Gröbner basis computations
presentation of scientific results on linear algebra for Gröbner basis computations
modular approaches to Gröbner basis computations which allow to swap linear algebra packages
approaches to parallelization of linear algebra routines on multicore machines, multiple machines and GPUs.
suitable benchmark and test matrices, ideals and their format.

Invited Speakers

Brice Boyer (Grenoble, France)
Michael Brickenstein (Oberwolfach, Germany)
Daniel Cabarcas (Darmstadt, Germany)
Jean-Charles Faugère (Paris, France)
Bradford Hovinen (Munich, Germany)
Sylvain Lachartre (Paris, France)
Emmanuel Thomé (Nancy, France)

The workshop will feature mathematical talks, presentations on software and coding sprints.

Registration

There is no registration fee for the workshop. Please email the organizers beforehand if you intend to participate.

It is strongly recommended that participants bring their own laptop for use during the coding sprints.

More information regarding this event is available at http://wiki.lmona.de/events/elagb